How to decide your sample size when the power calculation is not straightforward

A question I’m most often asked (other than excluding those pesky outliers) is “what is a suitable sample size for my experiment?”. It’s an age-old question that is fundamental when applying the 3Rs in animal research. If too few animals are used, the scientific validity of the experiment and the reliability of the results will be brought into question. If too many animals are used, the risk of making a false positive conclusion increases (statistically significant effects are declared that are of no practical relevance), not to mention the ethical issues. Many funders and journals are now requiring information about how sample sizes were selected, which is a really important step.

By highlighting questions I’m commonly asked, I’ll go through a few options available to the animal researcher.

As described on the EDA information pages, the following parameters are taken into consideration when performing a power calculation to determine the sample size:

• The size of the effect you are interested in (or ‘signal’, which the researcher needs to define).
• The risk of a false positive (or significance threshold, usually fixed at 5%).
• The statistical power (or the ability to spot a true effect).
• The variability of your data – the more variable your data is the more animals you’ll need, so it’s worth taking time to think about your experimental design/statistical analysis to see if you can identify ways of reducing the variability.

I often hear “we always use n=6” or “the other researchers use n=6, so shall we”. Needless to say, this is not a recommended approach. You cannot simply copy someone else’s sample sizes; you need to assess the variability of data generated in your lab, under your experimental conditions and using your protocols. Even if your supervisor or manager says “use n=6”, make sure you question them and check it is suitable!

That said, previous experiments from other labs using the same animal model can provide useful data on which to base an estimation of variability. In an ideal world, you will have an idea about the variability of your data, perhaps from a pilot study or other work done in your lab recently, as well as an idea about the size of effect you consider to be biologically relevant. If you don’t have any data yourself, then perhaps you can get a rough idea from the literature. There has been a push recently for authors to describe their reasoning behind the sample sizes used and I think this gives more confidence to a reader reviewing their work. When quoting results from a sample size assessment, the variability estimate that has been used should always be stated.

Power curves are a useful visual tool to assess sample size and power for various biologically relevant effects. They can be easily generated within InVivoStat’s Power Analysis module. In the figure below, it can be seen that in order to achieve a statistical power of 80% (Y-axis), where the effect size is an absolute change of size 3 (green line), n=8 animals will be required (reading down to the X-axis).

If the effect size you are interested in detecting is an absolute change of less than 2 (blue line), it will not be possible to power the experiment correctly. In this instance, you should not run the experiment but investigate ways to reduce the variability in the animal model.

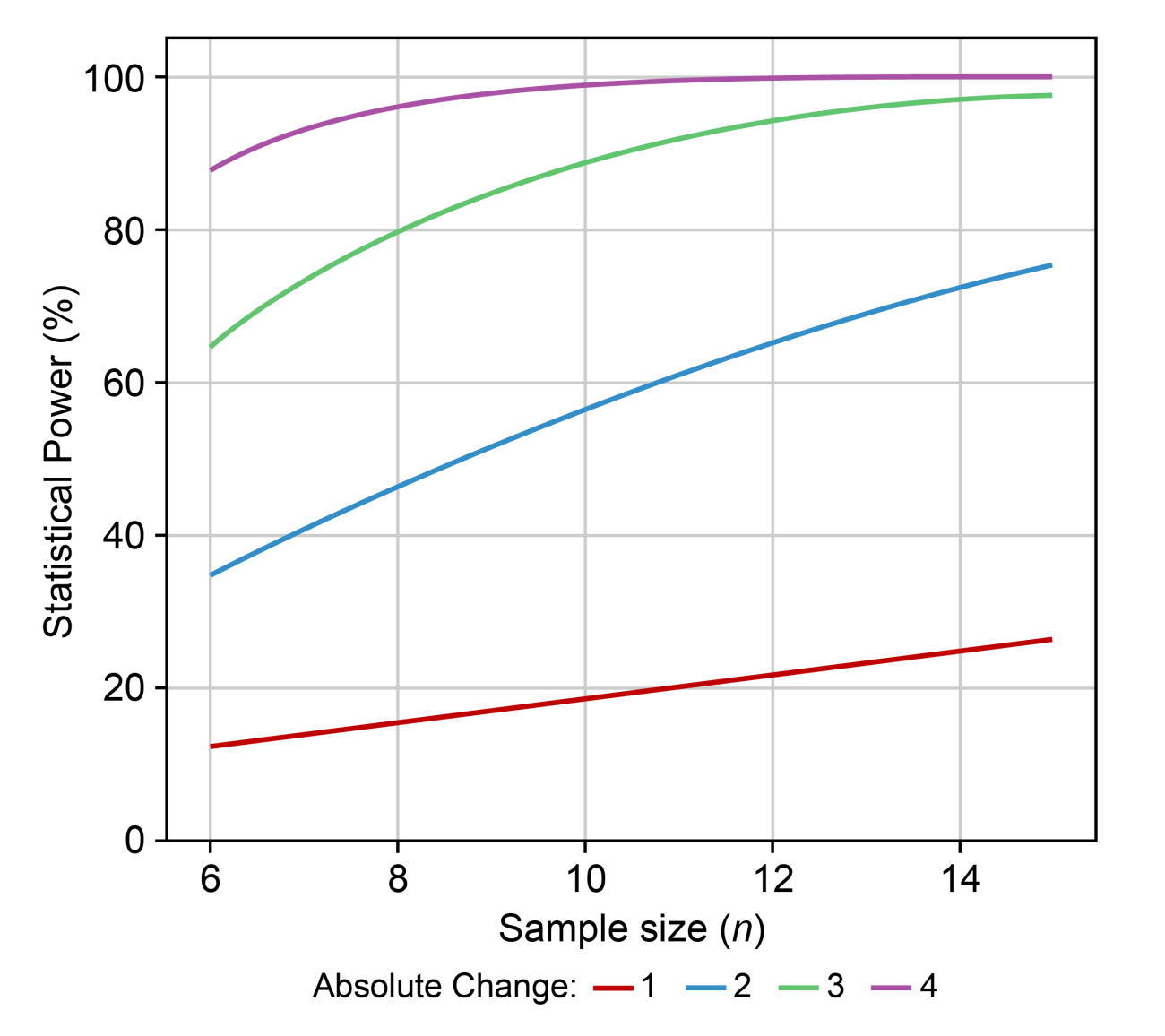
Remember these power curves are based on an estimate of the variability – which may or may not be reliable. I always advise researchers to re-generate this graph anew using the more recent estimate of variability obtained from their completed study data. These new plots shouldn’t be used to do a ‘post-hoc power analysis’, but comparing to the original power curves to the new ones will give you an idea how reliable the original power analysis was. In theory, if the power curves are reliable, then whenever you get new data you should always get a similar looking plot.

I’m often asked this question when investigating sample size. It’s a difficult question to answer, but I think you should have some idea of the size of effect you are looking for before you start! You don’t need to settle on a single value (as highlighted in the plot above) but you do need a suitable range. I start by asking:

• What is the smallest effect that could be of biological relevance?
• What is the largest effect expected when testing a positive control in the animal model?

This gives us a working range that can be reduced and fine-tuned.

In deciding on the effect size that would be of biological relevance, one key question to ask is: what is the minimum effect I would need to see to consider it worth taking forward in further research?

For example, if you are investigating a drug improving symptoms in a stroke model, you might only be interested in at least a 30% change because that’s the level of protection afforded by drugs in the clinic, so as a researcher you are only interested in treatments which have a bigger effect.

Or, say you are planning to silence a gene using RNAi – you first need to decide what efficacy will be satisfactory. Would a knockdown of, say, 50% be sufficient to have a biological effect, or do you need to aim for 90% efficacy? It’s useful to have background information about the gene and its abundancy, function, the turnover time of the gene product, other gene products that could have overlapping functions, and so on.

The above approaches rely on you having an idea of the variability of your data. If historical data is not available, the literature can be used to estimate the variability from similar experiments or models. However, you must take special care as small changes in experimental procedures can cause unexpectedly large alterations in variability. If no information is available to inform your experimental design, then there are alternatives, for example Cohen’s d – a standardised effect size which can be used instead. There are particular rules for using the Cohen’s d approach, and it is usually not as accurate as using measured data. For more information on this, see this section on variability.

Many animal experiments do have multiple responses as we want to get the most information from one experiment. For example, we could be measuring markers of inflammation, such as chemokines, cytokines, CRP, IL-1, IL-4, IL-6, IL-10, TNF-α, TGFb, ICAM-1, IFN-γ, etc. at the same time. However, each response will probably have different biologically relevant effect sizes and different levels of variability. So, inevitably the statistical power will vary between responses for a given sample size. We need to take a leaf out of the clinical trials book here and decide on which outcome measures are essential to test the hypothesis, and which are desirable, then choose a primary outcome measure to calculate the sample size. If secondary outcome measures are considered essential, power calculations should be performed for each of these measures to ensure that the sample size chosen will provide adequate power for all essential outcome measures.

This scenario, which I’ve seen in in vitro more than in in vivo studies, plays out something like this: the researcher performs a set of experiments and analyses the results. If they see something “interesting” but not statistically significant in the results, they then test another batch of cells (and potentially keep going until they reach the ‘promised land’ of p<0.05).

This is known as P-hacking [1], and is really not recommended, as it substantially increases your risk of obtaining a false positive result. It also shows a lack of understanding of experimental design and randomisation. The design should be planned in advance (for example, by using the EDA), including the choice of sample size, and that plan should be adhered to so that the whole process is performed in a controlled and unbiased way.

I sometimes get asked this question and I think it’s possibly down to a misunderstanding of the concepts of independence and blocking. The logic is that if the researcher repeats a (potentially small) experiment three times, and observes the same trends in all three experiments, then there is ‘strong’ evidence of an effect. In which case there is an assumption that power calculations are not necessary.

There are a couple of issues with this logic. Firstly, if the individual experiments are underpowered, then all three might reveal the same false positive trend as none of the experiments are individually reliable. Alternatively, perhaps the underpowered individual experiments fail to identify the true effect due to the variability. This situation is made worse because the tests themselves may not be truly independent: the experiments may have been performed by the same researchers following the same protocol in the same lab, just on different days (ensuring close agreement between experiments). As a result, the evidence collected over three studies may not be as conclusive as the researcher imagines.

One option would be to analyse the data from the three experiments as one single (larger) dataset. The statistical power will be higher (and the results more reliable) as the sample size is now three times greater. However, this is still not ideal and a more effective approach is to use a block design (each small experiment being a block) and calculate the sample size needed for the entire experiment with a power calculation. In this scenario, it may be possible to use fewer animals than in the three separate experiments while increasing the statistical power.

If you have an estimate of the variability, then an alternative strategy that has the potential to increase statistical power is to use a group-sequential design. With a group-sequential design, interim analyses, usually two or three, are pre-planned into the study design and experiments can be terminated early if a statistically significant effect has been achieved (or no effect observed), thus saving animals. When carrying out multiple analyses, the risk of finding a false positive increases, and so the significance level has to be reduced from 5% to account for this: various methods are available to do this. Neumann et al. [2] describe a scenario where two groups are compared (effect size = 1) using either a traditional design (with n=18 per group) or a group-sequential design. In the latter, interim analyses are performed when n=6 animals have been assessed and then potentially when n=12 and n=18 have been tested (depending on the outcome of previous interim analyses). Using this approach led to an average saving of 20% of the animals used without a decrease in statistical power.

Finally, a question from me to finish.

When deciding on the sample size, it is worth first considering what question you are trying to answer. Many traditional power analysis approaches assume that the purpose of the experiment is to compare two (or more) experimental group means, using ANOVA or t-tests. Such assessments require suitable numbers of animals in each group. But are you really just trying to compare one treatment group back to control? Perhaps you are really interested in estimating/understanding the underlying dose-response relationship itself. If so, then the choice of the experimental design, and hence the sample size per group, may be different.

For example, it turns out that if you are interested in understanding the dose-response relationship, and want to identify the ED₅₀, then using a design with more dose groups and fewer animals per group, perhaps as low as three per group, is a better design to use than more orthodox designs/sample sizes. Bate and Clark (2014, Section 3.6.2.2) give such an example. As another example, if screening the overall effect of multiple factors is the purpose of the study, then using a factorial design (with n=1 or 2 animals per combination of the levels of the factors) may be an appropriate design – see [3].

In general, the questions researchers are trying to answer are often complex. If this is the case then the help of a statistician may be required, for example to run simulations to identify the best design/sample size. However it is done though, in principle we should always try to align the choice of experimental design with the questions we are trying to answer.

On a final note, there is a YouTube video doing the rounds that looks slightly odd at first but is a good representation of what happens when two people speak different research languages. A scientist comes to a statistician and asks their advice on justifying the sample size. The statistician asks many pertinent questions and the researcher tries to provide some additional information which is useful in their eyes, but at the same time the researcher’s reply is always “I need to use n=3”. Hopefully such conversations will become less frequent in future!